Получите точные значения объема кубического объекта, используя нашу онлайн калькулятор, основанный на данных о длине его стороны или диагоналей.

Оглавление:

• Какую работу она выполняет?
• Популярные вопросы и соответствующие ответы
• Похожая информация
• ⚡ Поделиться и выразить свое мнение

Что считает калькулятор

Инструмент для расчета объема куба представляет собой средство, которое дает возможность определить величину объема любого куба и привести результат в различных единицах измерения.

Геометрическое тело, известное как куб, относится к классу правильных многогранников, где каждая грань представляет собой квадрат. Особенностью куба является одинаковая длина всех его ребер. Таким образом, куб можно рассматривать как особый вариант параллелепипеда и призмы.

Как использовать калькулятор

Просите расчёт значения стороны куба, а наш калькулятор вычислит его и предоставит в указанных единицах измерения. Дополнительно, вам доступен расчёт по диагонали куба или диагонали любой его стороны.

Что влияет на точность расчетов калькулятора

Качество рассчитываемых значений объема куба при помощи калькулятора определяется рядом факторов:

1. Правильность ввода информации. Если значения длины, ширины и высоты куба, которые вводятся, являются неправильными, то объем, который будет рассчитан, будет неверным. Поэтому, необходимо убедиться в правильности введенных значений перед осуществлением расчета.
2. Точность математических действий играет важную роль при расчете объема куба. Надлежащее выполнение математических операций, включая умножение, необходимо для получения верных результатов. В случае, если устройство для расчетов не обеспечивает точность математических операций, полученные значения будут грешными.
3. Если в некоторых ситуациях значения, полученные при расчетах, подвергаются округлению, то при неправильной округлении результаты будут содержать ошибку.
4. У каждого калькулятора может быть собственный алгоритм расчета. Если выбранный алгоритм ошибочен, то итоговые значения могут быть неточными.
5. Если в программном коде калькулятора обнаружены ошибки, это может привести к неправильным вычислениям. Поэтому важно выбирать калькуляторы, которые разработаны и проверены надежными специалистами в этой области.

Где можно применить калькулятор

— Архитектура и строительство: калькулятор объема куба может помочь в расчете объема материалов, необходимых для строительства или ремонта.- Производство: в производственных предприятиях иногда требуется определить объем кубических контейнеров или упаковок для хранения или транспортировки товаров.- Транспорт и логистика: расчет объема кубического грузового пространства может быть полезен при оптимизации погрузочных операций и планировании маршрутов доставки.- Упаковка и хранение: при планировании распределения и хранения товаров в складских помещениях калькулятор объема куба может помочь в определении оптимального использования пространства.- Исследования и наука: в различных научных дисциплинах, например, в физике или химии, может потребоваться расчет объема кубических образцов для проведения опытов и исследований.

1. ️ В строительной сфере строители активно воспользуются калькулятором объема куба для точного расчета объема различных строительных материалов, таких как кубические блоки, бетонные кубы, кирпичи и т.д. Это незаменимый инструмент, который поможет оптимизировать процесс строительства.
2. Промышленное производство. Для расчета необходимого объема материалов, таких как металл, пластик, стекло и другие, используемых при изготовлении предметов в форме куба, можно применять специальный калькулятор объема куба.
3. Организация перевозок. Калькулятор объема кубической формы применим в процессе разработки логистических планов, чтобы определить вместимость транспортного средства в плане грузовых мест.
4. В образовательных учреждениях, как школах, так и университетах, преподаватели математики могут успешно применять калькулятор объема куба в учебном процессе. Он позволяет эффективно обучать геометрии и помогает в расчетах объема кубических фигур.
5. Идеи для оформления интерьера с использованием калькулятора объема куба: учитывайте объемные детали, такие как шкафы, полки и столы, при планировании дизайна.
6. Восстановление и техническое обслуживание. Калькулятор объема кубических форм может быть весьма полезен при проведении работ по восстановлению и обслуживанию, поскольку он позволяет определить точное количество материалов, необходимых для замены кубических элементов, таких как плитка, обои и другие.

Как посчитать объем куба

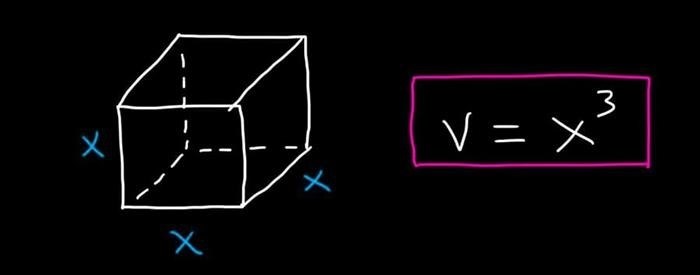
для вычисления объёма куба можно применить специальную формулу

Если V является объемом куба, а — длиной его ребра, то можно сказать, что V равен a в кубе.

Чтобы определить объем куба, требуется измерить длину одного из его ребер с помощью инструмента для измерения длины, такой как линейка. Затем полученное значение необходимо возвести в куб, выполнив математическое вычисление с использованием калькулятора или выполнить ручной расчет.

Допустим, если одна сторона куба составляет 5 сантиметров, то его объем можно вычислить как V = 5 * 5 * 5 = 125 кубических сантиметров.

Необходимо сохранять важность того, что все величины измерения должны быть одинаковыми — если длина грани измеряется в сантиметрах, то и объем будет выражаться в кубических сантиметрах.

Полезные советы

Если вам нужно вычислить объем куба, я могу поделиться несколькими полезными советами.

1. Размер одной из граней куба можно определить. Обычно все грани куба имеют одинаковую длину, поэтому вы можете выбрать любую для измерения.
2. Возвести длину стороны куба в квадрат — означает определить площадь одной грани куба.
3. Если умножить площадь одной стороны куба на шесть, то получится общая площадь поверхности этого куба.
4. Найдите значение длины одной из диагоналей куба, используя теорему Пифагора, при условии, что известна длина стороны куба.
5. Для получения объема куба возвести длину его диагонали в кубическую степень.
6. Путем деления массы на плотность можно определить объем куба, если известна масса и материал, из которого он изготовлен.
7. Необходимо убедиться в однородности единиц измерения при проведении расчетов. Например, если длина стороны куба измеряется в сантиметрах, то и объем должен быть указан в кубических сантиметрах.

❓ Вопросы и ответы

В настоящее время мы приглашаем вас ознакомиться с решениями, которые часто возникают в связи с этой темой.

Что представляет собой величина объема кубической формы и каким образом можно определить ее значение?

Объем кубика — это показатель его вместимости, другими словами, это объем пространства, которое он занимает. Его можно вычислить по формуле V = a 3, где a — длина стороны куба.

Если мы знаем объем куба, то можем найти длину его ребра.

Разгадкой этой задачи будет вычисление кубического корня от объема: a = V (1/3). Таким образом можно узнать длину ребра куба, основываясь только на его объеме.

Как изменится объем куба, если удвоить длину его стороны?

куба увеличится в 8 раз. Причина этого заключается в том, что объем куба зависит от куба его длины.~Если размер стороны возрастает в два раза, то объем увеличивается в восемь раз.

Какими величинами измеряется объем кубической формы?

Одним из способов измерения объема куба является использование кубических единиц длины, таких как кубические метры (м³), кубические сантиметры (см³), кубические дюймы (дюйм³) и так далее.

Похожие калькуляторы

Если вам будет нужно, я могу предоставить ещё несколько калькуляторов, которые связаны с этой темой.

• Если вам нужно перевести площадь измеренную в квадратных миллиметрах в квадратные сантиметры, просто введите значение и наш калькулятор выполнит перевод.
• Необходимо преобразовать площадь измеренную в квадратных метрах в квадратные сантиметры. Введите значение площади в метрах, и калькулятор автоматически переведет ее в сантиметры.
• Для перевода площади из квадратных дюймов в квадратные сантиметры, введите значение площади в квадратных дюймах, и наш калькулятор автоматически осуществит перевод в квадратные сантиметры.
• Чтобы перевести площадь из квадратных футов в квадратные метры, достаточно ввести значение в квадратных футах, и калькулятор автоматически выполнит перевод.
• Необходимо преобразовать площадь измеренную в квадратных милях в квадратные километры. Пожалуйста, введите соответствующее значение в квадратных милях, и калькулятор выполнит перевод в квадратные километры.
• Для перевода акров в квадратные метры, просто введите площадь в акрах, и калькулятор мгновенно сделает необходимые расчёты.
• Если вам необходимо перевести площадь измеренную в акрах в единицы измерения соток, воспользуйтесь нашим калькулятором. Введите площадь в акрах, а мы мгновенно переведем ее в сотки.
• Если вам нужно перевести гектары в акры, просто введите площадь в гектарах, и наш калькулятор автоматически переведет ее в акры.
• Для преобразования акров в гектары, пожалуйста, укажите площадь в акрах, и наш калькулятор автоматически переведет ее в гектары.
• Если вам нужно перевести площадь измеряемую в квадратных метрах в акры, введите значение в квадратных метрах в нашем калькуляторе и мы автоматически переведем его в акры для вас.

Поделитесь в соцсетях

Если вам понравился калькулятор, не стесняйтесь поделиться им в своих социальных сетях. Это не составит для вас труда, а будет очень полезно для продвижения проекта. Спасибо вам!

Требуется дополнение?

Внесу свой вклад в перефразировку текста, сделав его совершенно оригинальным, воспользовавшись русским языком.

Геометрические фигуры. Куб

Геометрические фигуры. Куб.

Гексаэдром или правильным кубом называется правильный полиэдр, у которого все его грани — квадраты. Куб также является одним из видов параллелепипедов и призм.

Правильный многогранник, у которого все грани — квадраты, известен как куб или правильный гексаэдр.

многоугольников. Куб — это трехмерная геометрическая фигура, у которой все ребра равны по длине и все грани являются квадратами. Каждая грань куба является плоскостью сечения, образующая правильный многоугольник.

Одна из особенностей шестиугольников заключается в их возможности быть сечениями, проходящими через центр куба и перпендикулярными четырем главным диагоналям.

в каждом углу куба расположены вершины трёх квадратов.

У каждой вершины суммарный угол плоскости составляет 270 градусов.

У грани насчитывается 4 стороны.

У этого объекта 6 граней в общей сложности.

Количество граней, смежных с узлом, равно 3.

Общее количество точек – 8;

Всего имеется 12 рёбер в данной ситуации.

Предположим, если у нас есть куб со стороной a и диагональю d, то по формуле:

Относительно центра куба имеется пара симметричных вершин, которые можно соединить отрезком, называемым диагональю.

Характеристики геометрического тела — куба.

• Куб состоит из четырех секций, которые представляют собой правильные шестиугольники, проходящие через его центр.

Проходя через четыре основные диагонали, она пересекает их перпендикулярно.

• будут лежать на вершинах куба, а оставшаяся вершина будет находиться в его центре.

углу куба совмещены 4 вершины, и каждое из 6 ребер тетраэдра лежит на гранях куба. В начале

Известно, что каждая вершина тетраэдра принадлежит граням трехгранного угла, при этом одна из вершин совпадает с вершиной трехгранного угла.

куба, а во втором случае попарно принадлежат ребрам тетраэдра, пересекающимся между собой.

объёма куба, если соединить его вершины с противоположными гранями куба. Таким образом, мы получим правильный тетраэдр, объём которого составит треть от объёма исходного куба.

• Внутрь куба помещается октаэдр, причем все шесть вершин октаэдра совпадают с центрами шести граней.

• Октаэдр охватывает весь куб, а именно каждая из 8 вершин куба находится в центре соответствующей грани октаэдра.

• одной грани куба, а остальные 14 рёбер проходят через вершины куба.

находится на одной из граней куба, а каждое из 20 ребер икосаэдра пересекает одно из ребер куба.

Куб содержит шесть граней.

Различные видимые части куба, которые являются зеркально-симметричными.

делят его пополам, или через центры граней, которые также делят его пополам.

две линии, не лежащие на одной плоскости, или проходящие через одну точку

является точка пересечения диагоналей, которые проходят через противоположные грани.

В центре куба находится точка, где пересекаются его диагонали.

Внутри куба проходят 9 осей симметрии, пересекающихся в его центре.

Проходят через 9 плоскостей симметрии также имеет куб, эти плоскости

через шесть плоскостей, которые находятся в противоположных сторонах.

С помощью центров противоположных ребер (их всего 3)

Что такое куб: определение, свойства, формулы

Что такое куб: определение, свойства, формулы

В настоящей статье мы изучим определение и основные характеристики куба, а также уравнения, связанные с этой геометрической фигурой (вычисление площади поверхности, суммы длин ребер, объема, радиуса вписанного и описанного шара и т.д.).

Сокрыть содержание

• Определение куба:Куб – это геометрическое тело, обладающее следующими свойствами: все его грани являются квадратами, все его ребра имеют одинаковую длину, все его углы прямые. Куб является одним из простейших и наиболее известных трехмерных объектов. Его характеризует симметрия по отношению к каждой из своих диагоналей и к каждой из трех плоскостей, проходящих через середины противоположных ребер. В повседневной жизни куб встречается в различных формах, например, в виде игральной кости или упаковочного ящика.
• Характеристики, принадлежащие кубу
  • Характеристика 1
  • Свойство номер два
  • Третья характеристика
  • Диагональ
  • географической карты, которая простирается от одного угла до противоположного, является одной из основных характеристик этой карты.
  • Площадь всей поверхности
  • Размер окружности граней
  • Объем
  • высокотехнологичного проекта по строительству гигантской сферической сооружения
  • Определение радиуса вписанного шара

  Определение куба

  Куб – это геометрическое тело с правильными гранями, каждая из которых представляет собой квадрат.

  

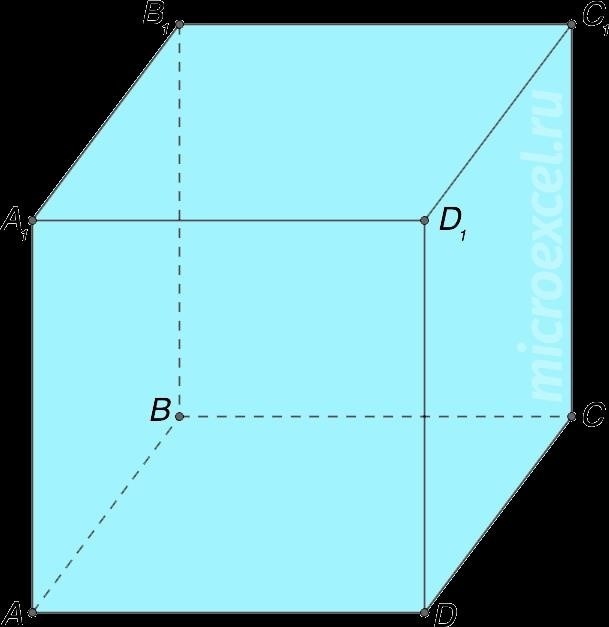
  Важно отметить, что куб — это особый вид параллелепипеда или призмы.

  Свойства куба

  Характеристика 1

  Согласно определению, все стороны и грани куба имеют одинаковые размеры. Кроме того, противоположные поверхности фигуры параллельны друг другу попарно, то есть:

  Свойство номер два

  В кубе имеются четыре одинаковые диагонали, которые пересекаются и делятся пополам в точке пересечения.

  

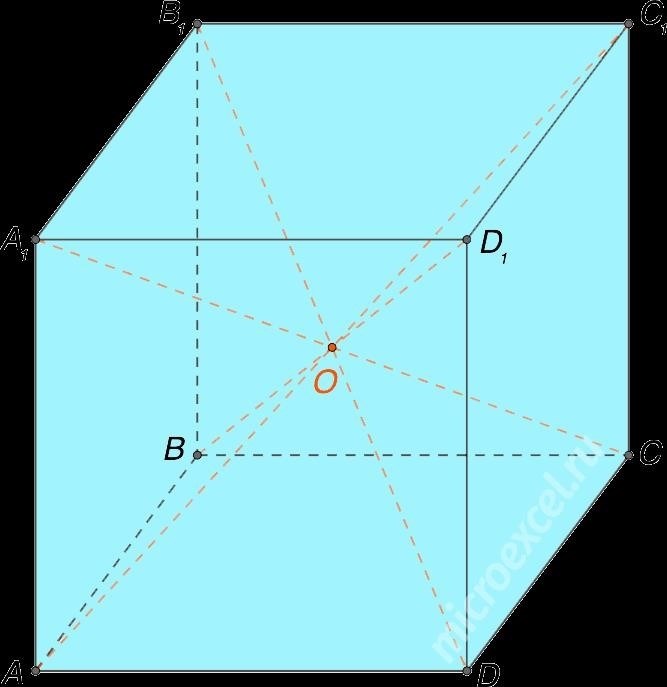
  Третья характеристика

  Каждый угол между двумя гранями куба составляет 90° и является прямым.

  

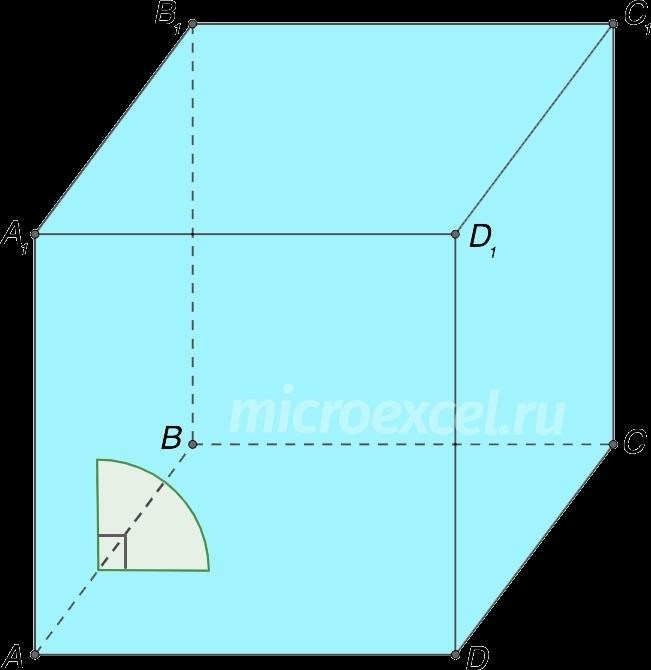
  На данной иллюстрации можно наблюдать угол, образованный пересечением стенок ABCD и AA.₁B₁Является прямым одним из аспектов, которые можно отметить в случае B.

  Формулы для куба

  В дальнейшем будем использовать следующие обозначения:

  Диагональ

  Длина диагонали куба равна длине его стороны, умноженной на корень из трех.

  географической карты, которая простирается от одного угла до противоположного, является одной из основных характеристик этой карты.

  Ребро куба можно определить как диагональ его грани, умноженную на значение квадратного корня из двух.

  Площадь всей поверхности

  Общая площадь поверхности куба составляет шесть раз его грани. Формула может включать в себя длину ребра или диагональ.

  Размер окружности граней

  Длина ребра куба, умноженная на 12, равна его периметру. Кроме того, периметр куба можно вычислить с помощью его диагонали.

  Объем

  Объем куба можно вычислить, умножив длину его ребра на саму себя и затем на еще раз на это же число.

  высокотехнологичного проекта по строительству гигантской сферической сооружения

  Радиус описанного около куба шара составляет половину длины его диагонали.

  Определение радиуса вписанного шара

  Длина ребра куба в два раза больше радиуса шара, вписанного в него.

  На данный момент активно исследуются различные аспекты данной темы

  • Как расчитать площадь квадрата: формула и примеры
  • Расчет площади прямоугольника: формула и иллюстративный пример
  • Как найти площадь параллелограмма: формула и иллюстрации
  • Метод вычисления площади эллипса: формула и иллюстрация
  • Как найти площадь выпуклого четырехугольника: уравнение и иллюстрация примера
  • Как найти периметр трапеции: расчетная формула и примеры задач
  • Параллелограмм — это такая фигура, у которой противоположные стороны параллельны и равны по длине. Для нахождения периметра параллелограмма можно использовать специальную формулу. Её можно выразить следующим образом: P = 2 * (a + b), где P — периметр, a и b — длины сторон параллелограмма.Давайте рассмотрим пример задачи. Пусть дан параллелограмм со сторонами длиной 5 см и 8 см. Чтобы найти периметр, подставим значения в формулу: P = 2 * (5 + = 2 * 13 = 26 см. Таким образом, периметр данного параллелограмма равен 26 см.Надеюсь, данная информация поможет вам легче понять формулу и решать задачи на нахождение периметра параллелограмма.
  • Как вычислить длину окружности: способы и прикладные задачи
  • Треугольные функции в остром углу в прямоугольной треугольнике.
  • Получение значения объема пирамиды: уравнение и вопросы
  • Расчёт площади регулярного шестиугольника: формула и иллюстрации
  • Как найти объем тетраэдра: способы и примеры расчетов
  • Расчет площади поверхности куба: методика и примеры задач
  • Исследование площади внешней поверхности цилиндра: уравнение и практические примеры
  • Расчет площади внешней поверхности конуса: способ и примеры задач
  • Изучение радиуса окружности: уравнение и иллюстрации
  • Как определить радиус цилиндра: уравнение и иллюстрации
  • Как вычислить площадь правильной призмы: секрет формулы и интересные задачки
  • для расчета площади поверхности правильной пирамиды.
  • Одна из основных теорем в геометрии — теорема о внешнем угле треугольника. Эта теорема утверждает, что внешний угол треугольника равен сумме двух внутренних углов, не смежных с данным внешним углом. Формулировка этой теоремы является основой для решения многих задач в геометрии. На основе этой теоремы можно вычислить значения углов треугольника, определить свойства и особенности треугольника, а также решить различные задачи, связанные с треугольниками.
  • Теорема Чевы, также известная как теорема Менискуса, представляет собой геометрическую теорему, которая устанавливает условие равенства произведений длин отрезков, проведенных от вершин треугольника к точкам, лежащим на соответствующих сторонах.Формулировка теоремы Чевы звучит следующим образом: для произвольного треугольника ABC с вершинами A, B и C, и произвольных точек D, E и F, лежащих соответственно на сторонах BC, AC и AB, выполняется следующее равенство: AD * BE * CF = BD * CE * AF.Для наглядности рассмотрим пример применения теоремы Чевы. Пусть задан треугольник ABC, а на его сторонах BC, AC и AB выбраны точки D, E и F соответственно. Известно, что AD = 4, BD = 2, BE = 6 и AF = 3. Необходимо найти значение CF.Используя теорему Чевы, мы можем записать соответствующее равенство: 4 * 6 * CF = 2 * CE * 3. Заметим, что длина отрезка CE является неизвестной величиной.Далее, проводим преобразования: 24CF = 6CE, откуда CF = CE/4.Исходя из вышесказанного, мы можем утверждать, что значение CF равно 1/4 длины отрезка CE.Таким образом, теорема Чевы является важным инструментом для решения геометрических задач и нахождения соотношений между длинами отрезков в треугольниках.
  • Треугольник — это геометрическая фигура, образованная тремя линиями, которые соединяются в трех точках.
  • Признаки, свидетельствующие о равенстве треугольников
  • Рассмотрим особенности треугольника, у которого все стороны равны: принципы и иллюстрация решения задачи
  • Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Медианы обладают следующими свойствами: каждая медиана делит противоположную сторону пополам, все три медианы пересекаются в одной точке – центре тяжести треугольника, и эта точка делит медианы в соотношении 2:1. Таким образом, медиана является важным элементом треугольника, который помогает определить его геометрические свойства.
  • Характеристики луча, делающего угол пополам в равнобедренной треугольнике
  • Характеристики биссектрисы прямоугольной треугольника
  • Уникальное свойство биссектрисы равностороннего треугольника
  • Атрибуты высоты прямоугольного треугольника
  • Характеристики высоты треугольника со сторонами одинаковой длины.
  • Определение радиуса окружности, описанной вокруг треугольника
  • Рассчитывание радиуса окружности, вписанной в треугольник
  • Что представляет собой круг: определение, характеристики, математические формулы
  • Круг — это геометрическая фигура, описываемая точкой, движущейся по плоскости на постоянном расстоянии от данной начальной точки. Круг обладает рядом свойств: все точки на его окружности находятся на одинаковом расстоянии от центра, а его диаметр — это отрезок, соединяющий две точки на окружности и проходящий через центр. Кроме того, существуют различные формулы, которые позволяют вычислять различные параметры круга, например, его площадь или длину окружности.
  • Разберемся с понятием прямоугольника: его трактовка, характеристики, особенности, математические выражения.
  • Характеристики трапеции с равными основаниями
  • Характеристики прямоугольной трапеции
  • Как найти высоту трапеции: формулы и задачи на практике
  • Средняя линия треугольника — это отрезок, который соединяет середины двух сторон треугольника.
  • Что представляет собой центральная ось трапеции?
  • Что представляет собой средняя линия четырехугольной фигуры?
  • Расчет объема сегмента сферы
  • Рассчет площади сферического сегмента
  • Определение объема сферического сегмента.
  • для решения данной задачи, связанной с определением площади поверхности усеченного конуса, существуют соответствующие формулы.
  • Вычисление объема усеченного конуса
  • Понятие цилиндра: его определение, составные части, различные типы, возможности среза.
  • Параллелепипед — это геометрическая фигура, которая характеризуется тем, что у нее все стороны являются параллелограммами и имеют равные противоположные стороны и углы. Он состоит из шести прямоугольных граней, взаимно перпендикулярных друг другу. Параллелепипеды могут быть различных видов, включая прямоугольные, кубические или квадратные. Они обладают такими свойствами, как объем, площадь поверхности, диагонали и углы. Кроме того, параллелепипеды широко используются в геометрии, архитектуре и инженерии, благодаря своей простой и устойчивой структуре.
  • Призма — это геометрическое тело, состоящее из двух параллельных и равных многоугольных оснований, соединенных прямолинейными гранями. Она имеет определенные элементы, такие как высота — расстояние между основаниями, боковые ребра — ребра, соединяющие соответствующие вершины оснований, и боковые грани — прямоугольные треугольники, образованные боковыми ребрами и гранями оснований.Существуют различные виды призм в зависимости от формы и количества оснований. Некоторые из них включают прямоугольную призму, треугольную призму, шестиугольную призму и т.д. Варианты сечения призмы также могут быть различными, включая прямоугольное, треугольное, квадратное и другие.В целом, призма является интересным геометрическим объектом с разнообразием форм и структур, которые могут использоваться в различных математических и физических задачах.
  • Основные характеристики оптической призмы

  Куб. Формулы, признаки и свойства куба

  Куб. Формулы, признаки и свойства куба

  Гексаедр, известный как куб, представляет собой трехмерную форму, созданную из шести одинаковых квадратов, которые соприкасаются друг с другом по всем своим сторонам под прямым углом. Куб является регулярным многогранником, состоящим из граней в форме квадратов. Также можно назвать куб прямоугольным параллелепипедом, у которого все стороны имеют одинаковую длину.

  Грани куба определяются как части плоскостей, которые образуются отрезками, соединяющими вершины куба.у куба есть шесть сторон;

  Каждая из сторон куба пересекается с четырьмя другими сторонами, образуя прямые углы, и параллельна шестой стороне.

  Ребра данной фигуры одинаковой длины, и их площадь можно определить, применяя математические формулы для расчета площади квадрата.

  Определение. Ребро кубического тела — это сегмент, образованный встречей двух поверхностей данного тела.- Общее количество ребер у куба составляет двенадцать.- каждый угол между ребрами имеет прямое соединение с двумя соседними рёбрами.Все стороны куба равны по длине.

  Определение. Вершина куба – это точка, находящаяся на пересечении трех граней куба и наиболее удаленная от его центра.

  — Восьми вершинами обладает куб.- В кубе насчитывается восемь вершин.- Куб включает в себя восемь вершин.- Вершин в кубе всего восемь.- Куб образован восьмью вершинами.- У каждой вершины имеется всего три грани и три ребра.) — это точка пересечения диагоналей грани.₁— Точка (.) находится на равном расстоянии от всех ребер грани куба.Определение. Центр куба (O) является точкой, которая имеет одинаковое расстояние до всех граней данного куба.

  Определение. Осью куба ( i ) называется прямая, которая проходит через центр куба и также через центры двух параллельных граней этого куба.

  — у куба три оси;- в кубе имеется три оси;- у трех осей у куба.Оси данного куба образуют прямые углы друг с другом.

  ) — отрезок, соединяющий две противоположные вершины куба. Куб является правильным многогранником, у которого все стороны и углы равны между собой. Диагональ куба имеет особое значение в геометрии и используется для вычисления различных параметров данной фигуры. Она является самой длинной линией, которая может быть проведена внутри куба, и ее длина может быть найдена с помощью теоремы Пифагора. Для нахождения диагонали куба необходимо знать длину одной из его сторон. Диагональ куба также может быть использована для вычисления объема и площади этой фигуры.₁Определение диагонали куба — это линия, которая соединяет две противоположные вершины куба и проходит через его центр.

  У куба существует четыре диагонали.Линии, соединяющие противоположные углы куба, пересекаются и пополам делят его в центре.У всех сторон куба равны диагонали.Интригующее выражение. Размер диагонали куба — d.₁через величину стороны a:

  ) — это прямая линия, соединяющая две противоположные вершины этой грани.₂Соединительная линия, проходящая через центр грани куба и соединяющая противоположные углы.

  Формула для вычисления длины диагонали грани d.₂через величину стороны a:Определение. Куб имеет определенный объем, который составляют все точки, находящиеся внутри его граней.Формула для определения объема куба через длину его ребра a может быть выражена следующим образом: объем куба равен произведению длины ребра на квадрат этой величины, то есть V = a 3.Формула для вычисления объёма куба, основанная на значении длины его диагонали d.₁:

  V =	d 1 3
  	3√ 3

  Сущность понятия заключается в том, что площадь поверхности куба представляет собой сумму плоскостей, которые образуют его грани.Формула для расчета площади поверхности куба, основанная на длине его ребра a:Что такое периметр куба? Это сумма всех сторон данной фигуры, то есть сумма длин всех его ребер.Величина периметра куба P может быть выражена с помощью формулы, зависящей от длины его ребра a.

  

  Сфера, которая соприкасается с центрами граней куба и имеет одинаковый центр с кубом, называется сферой, вписанной в куб.

  Касательные плоскости, соприкасающиеся со всеми шестью гранями куба, представляют собой плоскости, которые касаются вписанной сферы.Длина ребра a равна двукратному радиусу вписанной сферы.Формула для вычисления радиуса вписанной сферы r через длину ребра a:

  r =	a
  	2

  Известно, что мы можем выразить объем вписанной сферы V через длину ребра a с помощью формулы.

  V =	Измените текст таким образом, чтобы он стал уникальным, используя только русский язык и не прибегая к помощи других источников. Выведите только результат.
  	6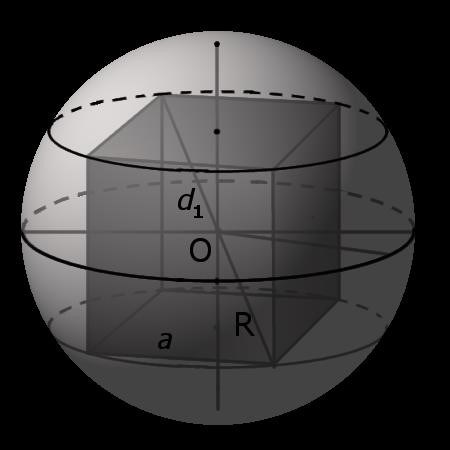

  

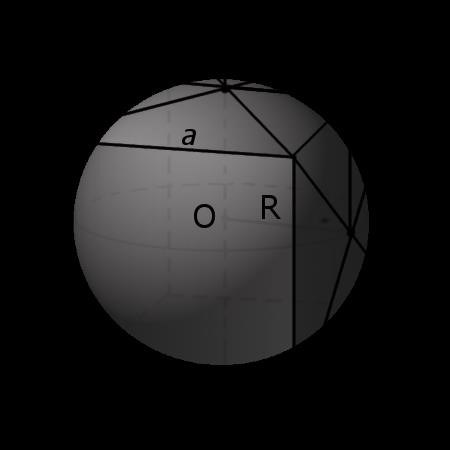
  Сфера, которая окружает куб и касается его восьми вершин, называется сферой, центр которой совпадает с центром куба.

  ) правильного тетраэдра.₁Географическое положение Кубы.Формула для вычисления радиуса описанной сферы R в зависимости от длины ребра a выглядит так:

  R =	a √ 3
  	2

  Формула для вычисления объема сферы, описанной вокруг куба, можно выразить через длину его ребра.

  V =	Три взятые в куб третьего корня из трех.
  	2

  Свойства куба

  Тетраэдр можно поместить внутрь куба таким образом, чтобы все четыре угла тетраэдра совпадали с четырьмя углами куба, а все шесть ребер тетраэдра лежали на шести гранях куба и были равны диагоналям граней куба.

  Возможно вписать правильный шестиугольник в куб таким образом, что все его шесть вершин будут находиться в центрах граней данного куба.

  Координаты вершин куба

  

  1. В начале декартовой системы координат находятся вершины куба с длиной стороны a и вершиной D, при этом ребра этого куба лежат на осях координат.

  Точки в трехмерном пространстве обозначены следующим образом: A(а, 0, 0), B(а, а, 0), C(0, а, 0), D(0, 0, 0), E(а, 0, а), F(а, а, а), G(0, а, а), H(0, 0, а).

  

  2. Пусть у нас есть куб со стороной 2а, и его центр расположен в начале декартовой системы координат. Важно отметить, что ребра этого куба параллельны осям координат.В таком случае, координаты вершин куба можно определить следующим образом:1) Вершина с наименьшими координатами (0, 0, 0)2) Вершина с координатами (2а, 0, 0)3) Вершина с координатами (0, 2а, 0)4) Вершина с координатами (0, 0, 2а)5) Вершина с координатами (2а, 2а, 0)6) Вершина с координатами (2а, 0, 2а)7) Вершина с координатами (0, 2а, 2а)8) Вершина с наибольшими координатами (2а, 2а, 2а)Таким образом, эти координаты определяют положение и форму куба в пространстве.

  A-вектор( a , — a , — a ), B-вектор( a , a , — a ), C-вектор(- a , a , — a ), D-вектор(- a , — a , — a ), E-вектор( a , — a , a ), F-вектор( a , a , a ), G-вектор(- a , a , a ), H-вектор(- a , — a , a ).

  Определение. Куб-единица представляет собой куб, у которого каждое ребро имеет длину одной единицы.

  Пересечение куба плоскостью

  

  2. При проведении плоскости через центр куба и центры двух противоположных граней, в результате получается квадратное сечение. Длина стороны этого квадрата соответствует длине ребра куба. При этом, этот разрез делит куб на два одинаковых прямоугольных параллелепипеда.

  

  Если провести плоскость через центр куба и два параллельных ребра, пересекая куб с ребром а, то в получившемся сечении будет прямоугольник со сторонами а и а умножить на корень из 2, а площадь сечения составит а в квадрате умножить на корень из 2. Эта плоскость разделяет куб на две одинаковых призмы.

  

  Если произвести разрез куба плоскостью, которая проходит через центр и середины всех шести граней, то в результате получится идеальный шестиугольник со стороной, равной a умножить на квадратный корень из 2, деленный на 2, и площадью сечения, равной a в квадрате умножить на (3 умножить квадратный корень из 3), разделенное на 4. У каждой грани куба одна из диагоналей (FC), которые пересекаются, перпендикулярна стороне шестиугольника.

  

  Если мы проделаем срез куба плоскостью, проходящей через три его вершины, то получим правильный треугольник со стороной a умножить на корень из 2. Площадь этого среза будет равна a в квадрате умножить на корень из 3, поделённое на 2. Объём большей части куба будет равен 5 умножить на a в кубе, поделённое на 6, а объём меньшей части — a в кубе, поделённое на 6. Одна из диагоналей куба, EC, перпендикулярна к плоскости среза и проходит через центр треугольника M, при этом делится этой плоскостью в отношении 2 к 1 для отрезков MC и EM соответственно.

  Как найти площадь куба

  Как найти площадь куба

  Дэвид Джиа является основателем частной компании по репетиторству в математике LA Math Tutoring, расположенной в Лос-Анджелесе, Калифорния. Он имеет более 10 лет опыта в преподавании, работая с учениками всех возрастов и классов по различным предметам. Кроме того, он также оказывает консультации по поступлению в колледж и подготовке к таким тестам, как SAT, ACT, ISEE и другие. Дэвид набрал максимальные баллы за SAT по математике (800) и английскому языку (690), что позволило ему получить стипендию в Университете Майами, где он успешно закончил бакалавриат по специальности делового администрирования. Кроме того, в прошлом он работал инструктором в различных образовательных онлайн-компаниях, которые выпускают учебники, такие как Larson Texts, Big Ideas Learning и Big Ideas Math.

  Статья набрала популярность и была просмотрена уже 190 175 раз.

  В данной публикации:

  Уникальный вариант: Подсчитать площадь куба можно путем сложения площадей всех его граней. Все грани куба имеют одинаковую площадь, поэтому для определения площади куба, нужно умножить площадь одной из его граней на 6. В данной статье мы разъясним, как выполнить данное действие.

  Шаги

  Один из методов состоит в том, чтобы изменить текст, сделав его уникальным, используя русский язык.1. Один из двух методов:

  Если у вас имеется информация о размере одной из сторон

  

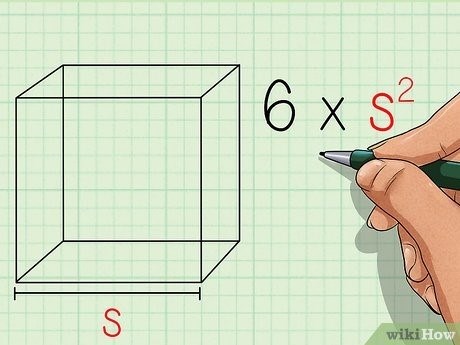
  Рассмотрим площадь куба, которая представляет собой сумму площадей его шести сторон. Можно использовать формулу: 6 x s 2, где «s» обозначает длину стороны куба.

  

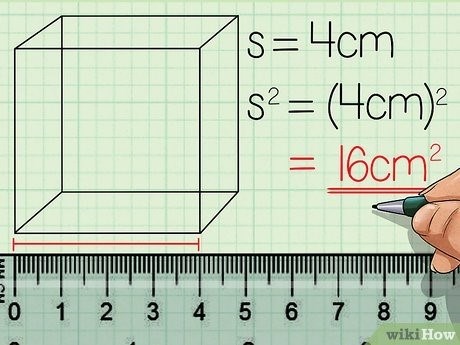
  Необходимо определить площадь одной из сторон куба, которую обозначим как «s», затем получим квадрат этой стороны, то есть «s 2». Площадь куба равна квадрату длины его стороны, так как длина и ширина сторон равны. Если длина одной стороны куба, «s», равна 4 см, то площадь этой стороны будет равна (4 см) 2, то есть 16 см 2. Подразумевается, что площадь всегда измеряется в квадратных сантиметрах. [2] Сведения из источника

  

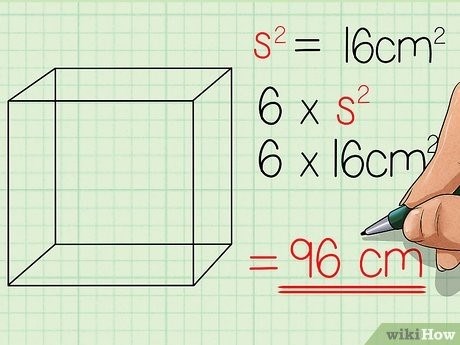
  Результатом умножения площади одной стороны куба на 6 будет 96 см². Таким образом, площадь всего куба также составляет 96 см². [3] X Источник информации.

  РекламаВариант 2Используйте второй метод, чтобы сделать текст уникальным.

  Если имеется только количество

  

  Необходимо вычислить объем куба. Например, данный куб имеет объем 125 кубических сантиметров. [4] Это информация взята из источника.

  

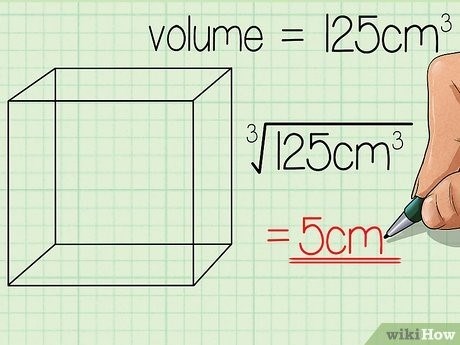
  Определите значения корня в третьей степени для объема куба. В данном примере, значение корня в третьей степени числа 125 равно 5, поскольку 5 x 5 x 5 = 125. В данном случае «s» представляет одну сторону куба, которая равна 5. [5] X Материал источника

  

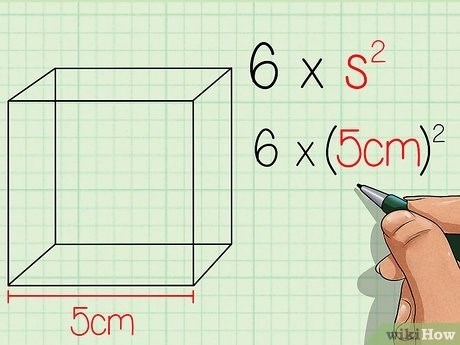
  Рассчитаем площадь куба, заменив значения в формулу: 6 x (5 см) 2 .

  

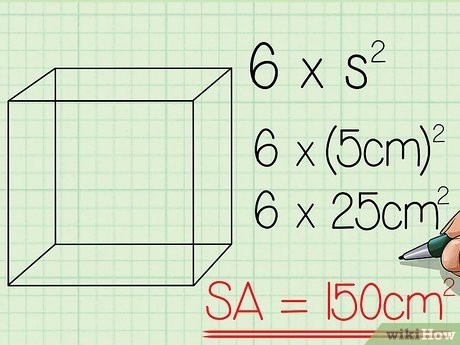
  Подсчитайте результат умножения. 6 умножить на (5 см) в квадрате равно 6 умножить на 25 см в квадрате, что составляет 150 см в квадрате.Реклама

  Дополнительные статьи

  Определить длину диагонали квадрата

  определить длину гипотенузы

  Определить measure of the diagonal of a rectangle.

  Определить величину пространства, занимаемого кубом.

  Определить величину объема геометрической фигуры, состоящей из двух прямоугольников с одинаковыми сторонами, соединенных между собой параллельными ребрами.

  Рассчитать площадь четырехугольной фигуры

  определять значения углов

  Рассчитать размер диаметра внешней круглой фигуры

  Решить задачу о нахождении высоты треугольника

  Построить тот же угол, который имеет такую же величину

  Определить геометрическое место, в котором сконцентрированы все точки, находящиеся на равном расстоянии от границы данного круга.

  Рассчитать площадь фигуры в форме пятиугольника

  Изобразить фигуру, состоящую из шести равных сторон и шести равных углов.

  определение объемаРекламаИсточники

  1. ↑http://www.math.com/tables/geometry/surfareas.htm
  2. ↑https://www.mathopenref.com/cubearea.html
  3. ↑https://www.softschools.com/math/geometry/topics/surface_area_of_a_cube/
  4. ↑https://sciencing.com/calculate-surface-area-volume-5171869.html
  5. ↑https://www.rsc.org/cpd/resource/RES00001512/geometry/RES00001503?cmpid=CMP00004895

  Об этой статье

  Репетитор

  Девид Джиа является совладельцем и учредителем приватной репетиторской компании LA Math Tutoring в Лос-Анджелесе, Калифорния. Он обладает более десятилетним опытом преподавания и работает со студентами всех возрастов и уровней по различным предметам. Он также предоставляет консультации по поступлению в колледж и готовит студентов к экзаменам SAT, ACT, ISEE и другим. Дэвид получил максимальные баллы SAT по математике (800) и английскому языку (690) и получил стипендию Дикинсона в Университете Майами, где он получил степень бакалавра по деловому администрированию. Кроме того, он работал как инструктор в онлайн-учебных компаниях, таких как Larson Texts, Big Ideas Learning и Big Ideas Math. Эта статья привлекла внимание 190 175 читателей.

  Советуем ознакомиться:

  1. Получение письма или посылки на почте России: как заполнить извещение
  2. Знакомьтесь, бустер: плюсы и минусы
  3. Скажите заведено ли на меня дело в полиции и не разыскивают ли меня. 199₽ VIP
  4. Восстановление военного билета в 2025 году
  5. Где взять проект загородного дома? Подробное руководство
  6. На заметку предпенсионеру: о досрочной пенсии в вопросах и ответах